Нахождение вектора, перпендикулярного данному вектору, примеры и решения, условие перпендикулярности векторов

Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.

Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.

Необходимое и достаточное условие перпендикулярности двух векторов

Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.

Определение 1

При условии значения угла между двумя ненулевыми векторами равным $90 °$ ( $\frac{π}{2}$ радиан) называют перпендикулярными.

Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?

Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.

Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.

Теорема 1

Скалярное произведение двух ненулевых векторов $\vec{a}$ и $\vec{b}$ равном нулю для выполнения равенства $(\vec{a}, \vec{b}) = 0$ достаточно для их перпендикулярности.

Доказательство 1

Пусть заданные векторы $\vec{a}$ и $\vec{b}$ перпендикулярны, тогда выполним доказательство равенства $(\overset{⇀}{a}, \vec{b}) = 0$ .

Из определения про скалярное произведение векторов мы знаем, что оно равняется произведению длин заданных векторов на косинус угла между ними. По условию $\vec{a}$ и $\vec{b}$ перпендикулярны, а, значит, исходя из определения, угол между ними $90 °$ . Тогда имеем $(\vec{a}, \vec{b}) = | \vec{a} | \cdot | \vec{b} | \cdot \cos (∠ (\vec{a}, \vec{b})) = | \vec{a} | \cdot | \vec{b} | \cdot \cos (90^{\circ}) = 0$ .

Вторая часть доказательства

При условии, когда $(\overset{⇀}{a}, \vec{b}) = 0$ доказать перпендикулярность $\vec{a}$ и $\vec{b}$ .

По сути доказательство является обратным предыдущему. Известно, что $\vec{a}$ и $\vec{b}$ ненулевые, значит, из равенства $(\vec{a}, \vec{b}) = | \vec{a} | \cdot | \vec{b} | \cdot \cos ∠ (\vec{a}, \vec{b})$ найдем косинус. Тогда получим $\cos ∠ (\vec{a}, \vec{b}) = \frac{(\vec{a}, \vec{b})}{| \vec{a} | \cdot | \vec{b} |} = \frac{0}{| \vec{a} | \cdot | \vec{b} |} = 0$ . Так как косинус равен нулю, можем сделать вывод, что угол $∠ (\vec{a}, \vec{b})$ векторов $\vec{a}$ и $\vec{b}$ равен $90 °$ . По определению это и есть необходимое и достаточное свойство.

Условие перпендикулярности на координатной плоскости

Раздел скалярного произведения в координатах демонстрирует неравенство $(\vec{a}, \vec{b}) = a_{x} \cdot b_{x} + a_{y} \cdot b_{y}$ , справедливое для векторов с координатами $\vec{a} = (a_{x}, a_{y})$ и $\vec{b} = (b_{x}, b_{y})$ , на плоскости и $(\vec{a}, \vec{b}) = a_{x} \cdot b_{x} + a_{y} \cdot b_{y}$ для векторов $\vec{a} = (a_{x}, a_{y}, a_{z})$ и $\vec{b} = (b_{x}, b_{y}, b_{z})$ в пространстве. Необходимым и достаточным условием перпендикулярности двух векторов в координатной плоскости имеет вид $a_{x} \cdot b_{x} + a_{y} \cdot b_{y} = 0$ , для трехмерного пространства $a_{x} \cdot b_{x} + a_{y} \cdot b_{y} + a_{z} \cdot b_{z} = 0$ .

Применим на практике и рассмотрим на примерах.

Пример 1

Проверить свойство перпендикулярности двух векторов $\vec{a} = (2, - 3), \vec{b} = (- 6, - 4)$ .

Решение

Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.

$(\vec{a}, \vec{b}) = a_{x} \cdot b_{x} + a_{y} \cdot b_{y} = 2 \cdot (- 6) + (- 3) \cdot (- 4) = 0$ . Условие выполнено, значит, заданные векторы перпендикулярны на плоскости.

Ответ: да, заданные векторы $\vec{a}$ и $\vec{b}$ перпендикулярны.

Пример 2

Даны координатные векторы $\vec{i}, \vec{j}, \vec{k}$ . Проверить, могут ли векторы $\vec{i} - \vec{j}$ и $\vec{i} + 2 \cdot \vec{j} + 2 \cdot \vec{k}$ быть перпендикулярными.

Решение

Для того, чтобы вспомнить, как определяются координаты вектора, нужно прочитать статью про координаты вектора в прямоугольной системе координат. Таким образом получаем, что у заданных векторов $\vec{i} - \vec{j}$ и $\vec{i} + 2 \cdot \vec{j} + 2 \cdot \vec{k}$ имеются соответствующие координаты $(1, - 1, 0)$ и $(1, 2, 2)$ . Подставляем числовые значения и получаем: $(\vec{i} + 2 \cdot \vec{j} + 2 \cdot \vec{k}, \vec{i} - \vec{j}) = 1 \cdot 1 + (- 1) \cdot 2 + 0 \cdot 2 = - 1$ .

Выражение не равно нулю, $(\vec{i} + 2 \cdot \vec{j} + 2 \cdot \vec{k}, \vec{i} - \vec{j}) \neq 0$ , а это означает, что векторы $\vec{i} - \vec{j}$ и $\vec{i} + 2 \cdot \vec{j} + 2 \cdot \vec{k}$ не перпендикулярны, так как условие не выполнилось.

Ответ: нет, векторы $\vec{i} - \vec{j}$ и $\vec{i} + 2 \cdot \vec{j} + 2 \cdot \vec{k}$ не перпендикулярны.

Пример 3

Даны векторы $\vec{a} = (1, 0, - 2)$ и $\vec{b} = (λ, 5, 1)$ . Найти значение $λ$ , при котором данные векторы перпендикулярны.

Решение

Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим

$a_{x} \cdot b_{x} + a_{y} \cdot b_{y} + a_{z} \cdot b_{z} = 0 \Leftrightarrow 1 \cdot λ + 0 \cdot 5 + (- 2) \cdot 1 = 0 \Leftrightarrow λ = 2$

Ответ: векторы перпендикулярны при значении $λ = 2$ .

Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.

Пример 4

Дан треугольник $А В С$ со сторонами $А В = 8, А С = 6, В С = 10$ см. проверить на перпендикулярность векторы $\vec{A B}$ и $\vec{A C}$ .

Решение

При перпендикулярности векторов $\vec{A B}$ и $\vec{A C}$ треугольник $A B C$ считается прямоугольным. Тогда применим теорему Пифагора, где $В С$ – гипотенуза треугольника. Равенство $B C^{2} = A B^{2} + A C^{2}$ должно выполниться. Отсюда следует, что $10^{2} = 8^{2} + 6^{2} \Leftrightarrow 100 = 100$ . Значит, $А В$ и $А С$ являются катетами треугольника $А В С$ , следовательно, $\vec{A B}$ и $\vec{A C}$ перпендикулярны.

Ответ: $\vec{A B}$ и $\vec{A C}$ перпендикулярны.

Нахождение вектора, перпендикулярного данному

Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.

Нахождение вектора, перпендикулярного данному в плоскости.

Ненулевой вектор $\vec{a}$ может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.

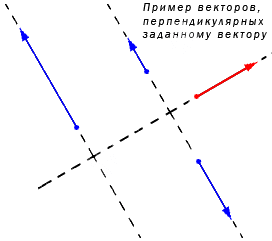
Нахождение вектора, перпендикулярного данному

Задан ненулевой вектор $\vec{a}$ , лежащий на прямой а. Тогда заданный $\vec{b}$ , расположенный на любой прямой, перпендикулярной прямой а, становится перпендикулярным и $\vec{a}$ . Если вектору $\vec{i}$ перпендикулярен вектор $\vec{j}$ или любой из векторов $λ \cdot \vec{j}$ при $λ$ равной любому действительному числу кроме нуля, то нахождение координат вектора $\vec{b}$ , перпендикулярному $\vec{a} = (a_{x}, a_{y})$ , сводится к бесконечному множеству решений. Но необходимо найти координаты вектора, перпендикулярного $\vec{a} = (a_{x}, a_{y})$ . Для этого необходимо записать условие перпендикулярности векторов в такой форме $a_{x} \cdot b_{x} + a_{y} \cdot b_{y} = 0$ . Имеем $b_{x}$ и $b_{y}$ , являющиеся искомыми координатами перпендикулярного вектора. Когда $a_{x} \neq 0$ , значение $b_{y}$ является ненулевым, а $b_{x}$ вычислим из неравенства $a_{x} \cdot b_{x} + a_{y} \cdot b_{y} = 0 \Leftrightarrow b_{x} = - \frac{a_{y} \cdot b_{y}}{a_{x}}$ . При $a_{x} = 0$ и $a_{y} \neq 0$ присваиваем $b_{x}$ любое значение кроме нуля, а $b_{y}$ находим из выражения $b_{y} = - \frac{a_{x} \cdot b_{x}}{a_{y}}$ .

Пример 5

Дан вектор с координатами $\vec{a} = (- 2, \sqrt{2})$ . Найти перпендикулярный данному вектор.

Решение

Обозначим искомый вектор как $\vec{b} (b_{x}, b_{y})$ . Найти его координаты можно из условия перпендикулярности векторов $\vec{a}$ и $\vec{b}$ . Тогда получим: $(\vec{a}, \vec{b}) = a_{x} \cdot b_{x} + a_{y} \cdot b_{y} = - 2 \cdot b_{x} + \sqrt{2} \cdot b_{y} = 0$ . Присвоим $b_{y} = 1$ и подставим: $- 2 \cdot b_{x} + \sqrt{2 \cdot} b_{y} = 0 \Leftrightarrow - 2 \cdot b_{x} + \sqrt{2} = 0$ . Отсюда из формулы получим $b_{x} = \frac{- \sqrt{2}}{- 2} = \frac{1}{\sqrt{2}}$ . Значит, вектор $\vec{b} = (\frac{1}{\sqrt{2}}, 1)$ является вектором, перпендикулярным $\vec{a}$ .

Ответ: $\vec{b} = (\frac{1}{\sqrt{2}}, 1)$ .

Если ставится вопрос о трехмерном пространстве, задача решается по такому же принципу. При заданном векторе $\vec{a} = (a_{x}, a_{y}, a_{z})$ существует бесконечное множество перпендикулярных векторов. Зафиксирует это на координатной трехмерной плоскости. Дана $\vec{a}$ , лежащая на прямой $a$ . Перпендикулярную прямой $a$ плоскость обозначаем $α$ . В этом случае любой ненулевой вектор $\vec{b}$ из плоскости $α$ перпендикулярен $\vec{a}$ .

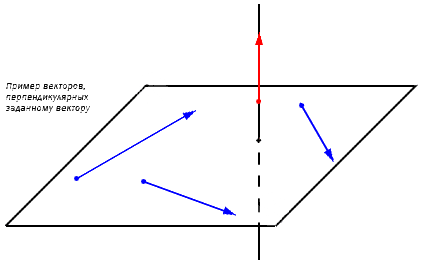
Нахождение вектора, перпендикулярного данному

Необходимо найти координаты $\vec{b}$ , перпендикулярного ненулевому вектору $\vec{a} = (a_{x}, a_{y}, a_{z})$ .

Пусть задан $\vec{b}$ с координатами $b_{x}, b_{y}$ и $b_{z}$ . Чтобы найти их, необходимо применить определение условия перпендикулярности двух векторов. Равенство $a_{x} \cdot b_{x} + a_{y} \cdot b_{y} + a_{z} \cdot b_{z} = 0$ должно выполняться. Из условия $\vec{a}$ - ненулевой, значит, одна из координат имеет значение не равное нулю. Предположим, что $a_{x} \neq 0$ , ( $a_{y} \neq 0$ или $a_{z} \neq 0$ ). Следовательно, имеем право разделить на эту координату все неравенство $a_{x} \cdot b_{x} + a_{y} \cdot b_{y} + a_{z} \cdot b_{z} = 0$ , получим выражение $b_{x} + \frac{a_{y} \cdot b_{y} + a_{z} \cdot b_{z}}{a_{x}} = 0 \Leftrightarrow b_{x} = - \frac{a_{y} \cdot b_{y} + a_{z} \cdot b_{z}}{a_{x}}$ . Присваиваем координатам $b_{y}$ и $b_{x}$ любое значение, вычисляем значение $b_{x}$ , исходя из формулы, $b_{x} = - \frac{a_{y} \cdot b_{y} + a_{z} \cdot b_{z}}{a_{x}}$ . Искомый перпендикулярный вектор будет иметь значение $\vec{a} = (a_{x}, a_{y}, a_{z})$ .

Рассмотрим доказательство на примере.

Пример 6

Дан вектор с координатами $\vec{a} = (1, 2, 3)$ . Найти вектор, перпендикулярный данному.

Решение

Обозначим искомый вектор за $\vec{b} = (b_{x}, b_{y}, b_{z})$ . Исходя из условия о перпендикулярности векторов, скалярное произведение должно быть равным нулю.

$(\overset{⇀}{a}, \overset{⇀}{b}) = 0 \Leftrightarrow a_{x} \cdot b_{x} + a_{y} \cdot b_{y} + a_{z} \cdot b_{z} = 0 \Leftrightarrow 1 \cdot b_{x} + 2 \cdot b_{y} + 3 \cdot b_{z} = 0 \Leftrightarrow b_{x} = - (2 \cdot b_{y} + 3 \cdot b_{z)}$

Если значение $b_{y} = 1, b_{z} = 1$ , тогда $b_{x} = - 2 \cdot b_{y} - 3 \cdot b_{z} = - (2 \cdot 1 + 3 \cdot 1) = - 5$ . Отсюда следует, что координаты вектора $\vec{b} (- 5, 1, 1)$ . Вектор $\vec{b}$ является одним из перпендикулярных векторов заданному.

Ответ: $\vec{b} = (- 5, 1, 1)$ .

Нахождение координат вектора, перпендикулярного двум заданным векторам

Нужно найти координаты вектора в трехмерном пространстве. Он перпендикулярен не коллинеаренным векторам $\vec{a} (a_{x}, a_{y}, a_{z})$ и $\vec{b} = (b_{x}, b_{y}, b_{z})$ . При условии коллинеарности векторов $\vec{a}$ и $\vec{b}$ в задаче достаточно будет найти вектор, перпендикулярный $\vec{a}$ или $\vec{b}$ .

При решении применяется понятие векторного произведения векторов.

Векторным произведением векторов $\vec{a}$ и $\vec{b}$ называют вектор, одновременно перпендикулярный и $\vec{a}$ и $\vec{b}$ . Для решения данной задачи применяется векторное произведение $[\vec{a} \times \vec{b}]$ . Для трехмерного пространства имеет вид $[\vec{a} \times \vec{b}] = | \begin{array}{l} \vec{a} \vec{j} \vec{k} \\ a_{x} a_{y} a_{z} \\ b_{x} b_{y} b_{z} \end{array} |$

Разберем подробнее векторное произведение на примере задачи.

Пример 7

Заданы векторы $\vec{b} = (0, 2, 3)$ и $\vec{a} = (2, 1, 0)$ . Найти координаты любого перпендикулярного вектора данным одновременно.

Решение

Для решения необходимо найти векторное произведение векторов. (Необходимо обратиться к пункту вычисления определителя матрицы для нахождения вектора). Получим :

$[\vec{a} \times \vec{b}] = | \begin{array}{l} \vec{i} \vec{j} \vec{k} \\ 210 \\ 023 \end{array} | = \vec{i} \cdot 1 \cdot 3 + \vec{j} \cdot 0 \cdot 0 + \vec{k} \cdot 2 \cdot 2 - \vec{k} \cdot 1 \cdot 0 - \vec{j} \cdot 2 \cdot 3 - \vec{i} \cdot 0 \cdot 2 = 3 \cdot \vec{i} + (- 6) \cdot \vec{j} + 4 \cdot \vec{k}$

Ответ: $(3, - 6, 4)$ - координаты вектора, одновременно перпендикулярного заданным $\vec{a}$ и $\vec{b}$ .