- 16 июля 2025
- 9 минут
- 3 392
Интегрирование простейших дробей
Статью подготовили специалисты образовательного сервиса Zaochnik.
Прежде, чем приступить к интегрированию простейших дробей для нахождения неопределенного интеграла дробно рациональной функции, рекомендуется освежить в памяти раздел «Разложение дроби на простейшие».
Найдем неопределенный интеграл .
Решение
Выделим целую часть, проведя деление столбиком многочлена на многочлен, учитывая тот факт, что степень числителя подынтегральной функции равна степени знаменателя:
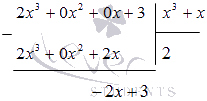
Поэтому . Мы получили правильную рациональную дробь , которую теперь разложим на простейшие дроби . Следовательно,
Мы получили интеграл простейшей дроби третьего типа. Взять его можно методом подведения под знак дифференциала.
Так как , то . Поэтому
Следовательно,
, где
Опишем методы интегрирования простейших дробей каждого из четырех типов.
Интегрирование простейших дробей первого типа
Используем для решения этой задачи метод непосредственного интегрирования:
Ответ:
Найдите множество первообразных функции .
Решение
Испльзуя правило интегрирования, свойства первообразной и таблицу первообразных, найдем неопределенный интеграл :
Ответ:
Интегрирование простейших дробей второго типа
Здесь также применим метод непосредственного интегрирования:
Необходимо найти неопределенный интеграл .
Решение
Ответ:
Интегрирование простейших дробей третьего типа
Первым шагом представим неопределенный интеграл в виде суммы:
Для того, чтобы взять первый интеграл, используем метод подведения под знак дифференциала:
Поэтому,
Мы получили интеграл . Проведем преобразование его знаменателя:
Следовательно,
Формула интегрирования простейших дробей третьего типа принимает вид:
Необходимо найти неопределенный интеграл .
Решение
Применим формулу:
Второй вариант решения выглядит следующим образом:
Ответ:
Интегрирование простейших дробей четвертого типа
Первым делом выполняем подведение под знак дифференциала:
Затем находим интеграл вида с использованием рекуррентных формул. Информацию о рекуррентных формулах можно посмотреть в теме «Интегрирование с использованием рекуррентных формул».
Для решения нашей задачи подходит рекуррентная формула вида .
Необходимо найти неопределенный интеграл .
Решение
Мы будем использовать для этого вида подынтегральной функции метод подстановки. Введем новую переменную
Получаем:
Пришли к нахождению интеграла дроби четвертого типа. В нашем случае имеем коэффициенты и . Применяем рекуррентную формулу:
После обратной замены получаем результат:
Ответ:
Математические онлайн-калькуляторы




