
Статью подготовили специалисты образовательного сервиса Zaochnik.
Деление натуральных чисел столбиком: правило, примеры
Содержание:
- 14 сентября 2023
- 12 минут
- 622
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком - удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем - многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Запись чисел при делении столбиком
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
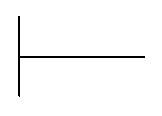
Пусть нам нужно разделить на , запишем:
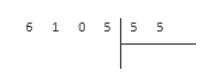
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
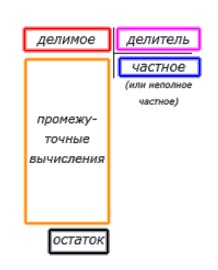
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
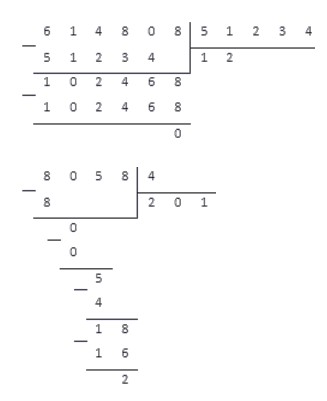
Деление столбиком на однозначное число
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа и в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что .
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
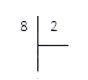
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число , на которое мы умножали делитель, записываем на место частного.
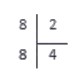
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае .
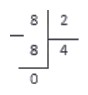
Данный пример - деление чисел без остатка. Число, получащееся после вычитания - это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число на натуральное число .
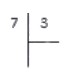
В данном случае, последовательно умножая тройку на получаем в результате:
Под делимым записываем число , полученное на предпоследнем шаге. По делителем записываем число - неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили .
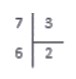
В завершение операции вычитаем из и получаем:
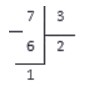
Данный пример - деление чисел с остатком. Неполное частное равно , а остаток равен .
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа на число . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
Алгоритм деления столбиком
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором - дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число - , так как первая цифра делимого меньше, чем делитель .

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как . Последовательно умножаем делитель на каждый член ряда натуральных чисел , включая нуль : и так далее. Делаем это, пока не получим в результате или число, большее чем . Когда в результате умножения получается число , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
.
Под выделенным числом записываем число , полученное на предпоследнем шаге. На место частного записываем множитель .

3. Столбиком вычитаем из , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.

4. Число меньше числа , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа записываем следующую цифру делимого - . В итоге отмечаем новое рабочее число - .
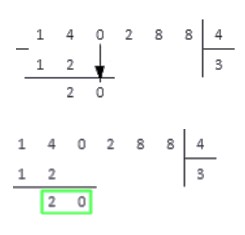
Пункты повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе . Умножая на получаем:
Так как мы получили в результе число, равное , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем - множитель, на который проводилось умножение.
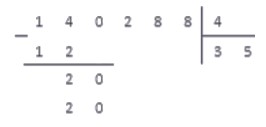
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: .
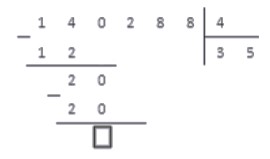
4. Мы не будем записывать число ноль, так как данный этап - еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае - число .
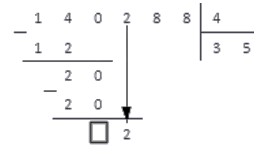
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
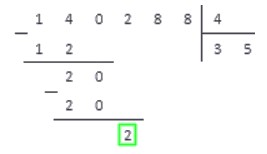
2. Умножаем делитель на и сравниваем результат с отмеченным числом.
Соответственно, под отмеченным числом записываем число , и под делителем в следующий разряд частного также записываем .
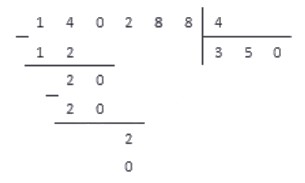
3. Выполняем операцию вычитания и под чертой записываем результат.
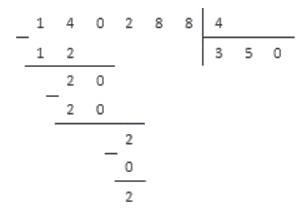
4. Справа под чертой добавляем цифру , так как это следующая цифра делимого числа.
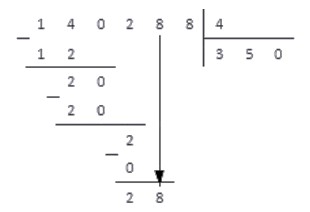
Таким образом, получаем новое работчее число - . Снова повторяем пункты алгоритма.
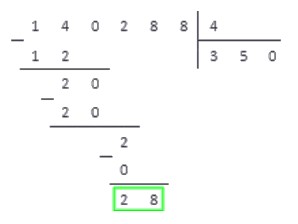
Проделав все по правилам, получаем результат:
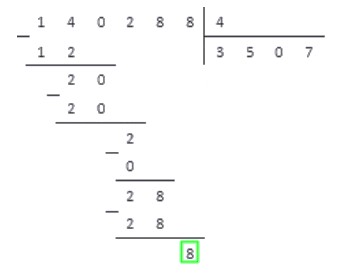
Переносим под черту вниз последнюю цифру делимого - . В последний раз повторяем пункты алгоритма и получаем:
В самой нижней строчке записываем число . Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа на является число . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Разделим натуральное число на натуральное число .
Запишем:
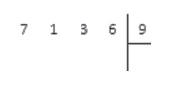
После второго, третьего и четвертого шага алгоритма запись примет вид:
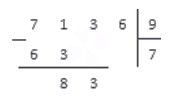
Повторим цикл:
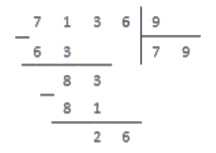
Последний проход, и поучаем результат:
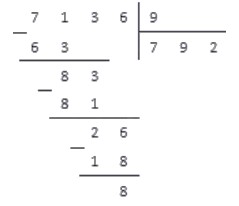
Ответ: Неполное неполное частное чисел и равно , а остаток равен .
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Разделим число на .
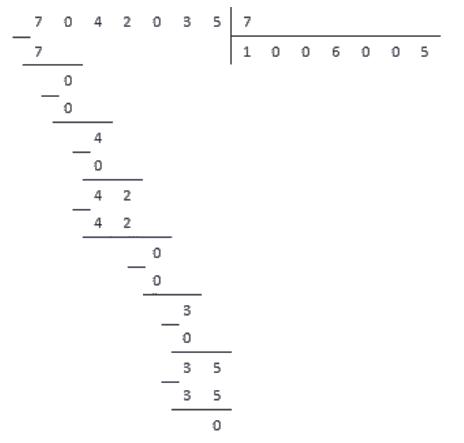
Ответ:
Деление многозначных натуральных чисел столбиком
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе - добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Разделим на .
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число .
, поэтому принимаем это число за рабочее и переходим к пункту аглоритма.
Умножаем на и получаем:
, поэтому под делителем записываем результат предпоследнего действия, а под делимым - множитель
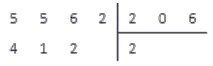
Выполняем вычитание столбиком
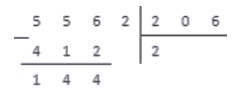
В результате вычитания имеем число . Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число - .
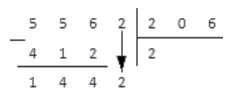
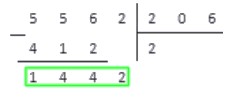
Повторяем с ним пункты . Получаем:
Под отмеченным рабочим числом записываем , а в следующий разряд частного записываем цифру - множитель.
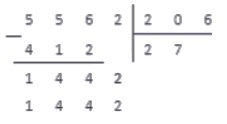
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
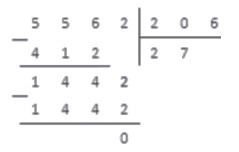
Ответ:
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Разделим натуральное число на .
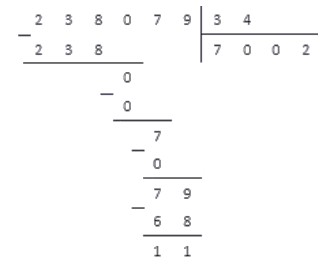
Ответ:
Навигация по статьям
