Вектор электрической индукции

Имеются пластины плоского конденсатора с зарядом $q$. Произойдет ли изменение вектора электрической индукции при заполненном воздухом пространстве между пластинами и диэлектрика с диэлектрической проницаемостью $\epsilon \ne {\epsilon }_{\upsilon ozd}$.

Решение

Поле конденсатора в первом случае характеризовалось вектором смещения $\left({\epsilon }_{vozd}=1\right)$, то есть $\overrightarrow{D_1}={\epsilon }_{vozd}{\epsilon }_0\overrightarrow{E_1}={\epsilon }_0\overrightarrow{E_1}$.

Необходимо заполнить пространство между пластинами конденсатора однородным и изотропным диэлектриком. При наличии поля в конденсаторе диэлектрик поляризуется. Тогда начинают появляться связанные заряды с плотностью ${\sigma }_{s\upsilon }$ на его поверхности. Создается дополнительное поле с напряженностью:

$E\text{'}=\frac{{\sigma }_{sv}}{{\epsilon }_0}$.

Векторы полей $\overrightarrow{E}\text{'}$ и $\overrightarrow{E_1}$ имеют противоположные направления, причем:

$E_1=\frac{\sigma }{{\epsilon }_0}$.

Запись результирующего поля с диэлектриком примет вид:

$E=E_1-E\text{'}=\frac{\sigma }{{\epsilon }_0}-\frac{{\sigma }_{s\upsilon }}{{\epsilon }_0}=\frac{1}{{\epsilon }_0}\left(\sigma -{\sigma }_{s\upsilon }\right)$.

Формула плотности связанных зарядов:

${\sigma }_{s\upsilon }=\chi {\epsilon }_{0}E$.

Произведем подстановку ${\sigma }_{s\upsilon }=\chi {\epsilon }_{0}E$ в $E=E_1-E\text{'}=\frac{\sigma }{{\epsilon }_0}-\frac{{\sigma }_{s\upsilon }}{{\epsilon }_0}=\frac{1}{{\epsilon }_0}\left(\sigma -{\sigma }_{s\upsilon }\right)$, тогда:

${\sigma }_{s\upsilon }=\chi {\epsilon }_{0}E$.

Далее выражаем из $(1.6)$ напряженность поля $Е$. Формула принимает вид:

$E=\frac{E_1}{1+\chi }=\frac{E_1}{\epsilon }$.

Отсюда следует, что значение вектора электрической индукции в диэлектрике равняется:

$D=\epsilon {\epsilon }_0\frac{E_1}{\epsilon }={\epsilon }_0{E}_1=D_1$.

Ответ: вектор электрической индукции не изменяется.

Была внесена пластина из диэлектрика с диэлектрической проницаемостью $\epsilon$ без свободных зарядов в зазор между разноименными заряженными пластинами. На рисунке $1$ показана при помощи штриховой линии замкнутая поверхность. Определить поток электрической индукции ${\Phi }_D$ через эту поверхность.

Решение

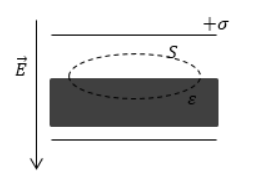
Рисунок $1$. Замкнутая поверхность

Формула записи потока вектора электрического смещения ${\Phi }_D$ через замкнутую поверхность $S$:

${\Phi }_D={\int }_S\overrightarrow{D}·d\overrightarrow{S}$.

Используя теорему Остроградского-Гаусса, можно сказать, что ${\Phi }_D$ равняется суммарному свободному заряду, находящемуся внутри заданной поверхности. Из условия видно отсутствие свободных зарядов в диэлектрике и в имеющемся пространстве между пластинами конденсатора, а поток вектора индукции равняется нулю.

Ответ: ${\Phi }_D=0$.

Изображена замкнутая поверхность $S$, проходящая с захватом части пластины изотропного диэлектрика на рисунке $2$. Поток вектора электрической индукции через нее равняется нулю, а поток вектора напряженности $>0$. Какой вывод можно сделать из данной задачи?

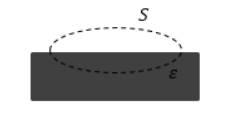
Рисунок $2$. Замкнутая поверхность с захватом части пластины изотропного диэлектрика

Решение

Из условия имеем, что поток вектора электрического смещения ${\Phi }_D$ через замкнутую поверхность равняется нулю, то есть:

${\Phi }_D=0$.

Если использовать теорему Остроградского-Гаусса, то значение ${\Phi }_D$ – это суммарный свободный заряд, находящийся внутри заданной поверхности. Следует, что внутри такой поверхности отсутствуют свободные заряды:

${\Phi }_D={\int }_S\overrightarrow{D}·d\overrightarrow{S}=Q=0$.

Имеем, что поток вектора напряженности не равен нулю, но он считается как сумма свободных и связанных зарядов. Отсюда вывод – диэлектрик содержит связанный заряды.

Ответ: свободные заряды отсутствуют, а связанные есть, причем с положительной их суммой.