
Статью подготовили специалисты образовательного сервиса Zaochnik.
Схема Горнера
Содержание:
- 28 декабря 2023
- 6 минут
- 177
В этой статье мы расскажем об удобной схеме решения примеров на деление многочленов. Если нам нужно вычислить коэффициент частного и остаток от деления многочлена на линейный двучлен , то удобно будет воспользоваться схемой (методом) Горнера.
Она заключается в создании особой таблицы и занесении в нее исходных данных:
| коэффициенты многочленов | |||||
Числа и будут нужными нам коэффициентами от деления на . Остаток обозначен здесь как . Иначе можно записать решение так:
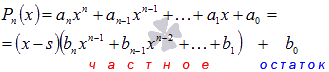
Теперь покажем , как именно применять эту схему на практике.
Условие: разделите многочлен на линейный двучлен , используя схему Горнера.
Решение
Заполним таблицу. У нас есть , равный единице, и коэффициенты .
| коэффициенты многочленов | |||||
Ответ: получили частное, равное , и остаток .
Во второй задаче мы обойдемся без подробных комментариев.
Условие: определите, можно ли разделить многочлен на двучлен без остатка. Вычислите частное.
Решение
Заполним таблицу согласно схеме Горнера.
| коэффициенты многочленов | |||||
В последней ячейке мы видим нулевой остаток, следовательно, разделить исходный многочлен на двучлен можно.
Ответ: частное будет представлять из себя многочлен .
Если , то можно говорить о делимости многочлена на двучлен , и мы имеем корень исходного многочлена, равный . Используя следствие из теоремы Безу, можем представить этот многочлен в виде произведения:
Благодаря этому схема Горнера хорошо подходит для тех случаев, когда нужно отыскать целые корни уравнений высших степеней, имеющих целые коэффициенты, или же разложить многочлен на простые множители.
Условие: решите уравнение . Разложите многочлен слева на отдельные множители.
Решение
Мы знаем, что целые корни уравнения (если они есть) нужно искать среди делителей свободного члена. Запишем их отдельно и проверим, используя схему Горнера.
| коэффициенты многочленов | |||||
Из данных таблицы видно, что единица не будет входить в число корней данного уравнения.
Дополним таблицу еще одним возможным корнем.
| коэффициенты многочленов | |||||
А вот подходит, значит, мы можем представить исходный многочлен как .
Проверяем делители дальше. Начнем с , поскольку возможно повторение корней, но в качестве коэффициентов будем брать значения последней строки:
| коэффициенты многочленов | |||||
Из этого следует, что не будет кратным (повторяющимся) корнем. Берем следующий вариант и вычисляем:
| коэффициенты многочленов | |||||
Число не входит в число корней уравнения. Дополним таблицу Горнера для :
| коэффициенты многочленов | |||||
Минус два будет корнем исходного уравнения. Мы можем записать многочлен так:
Третий и последний корень уравнения будет равен трем. Закончим заполнение таблицы, взяв значения последней полученной строки в качестве коэффициентов:
| коэффициенты многочленов | |||||
Из этого можно сделать вывод, что последняя полученная таблица, заполненная по методу Горнера, и будет решением нашего примера. Эту задачу можно было решить и делением многочлена на линейный двучлен столбиком, однако показанная здесь схема нагляднее и проще.
Ответ: , .
Навигация по статьям
