Производная, основные определения и понятия

Содержание:

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Данная статья рассматривает основные понятия, для решения задач с производными с одной переменной.

Определение 1

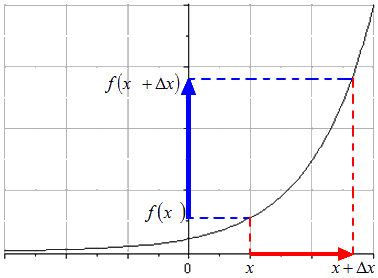
Пусть $х$ – это аргумент функции $f (x)$ и $∆ x$ возьмем малое число, не равное $0$ . Значение $∆ x$ называют приращением аргумента функции и читают как «дельта икс». На рисунке видно, что красная линия относится для изменений аргумента от значения $х$ до $x + ∆ x$ .

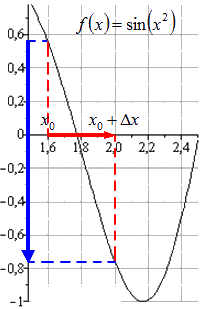
Производная, основные определения и понятия — Определение 2

Определение производной функции в точке

Когда функция вида $f (x)$ определена из промежутка $(a; b)$ , тогда $x_{0}$ и $x_{0} + ∆ x$ считаются точками данного промежутка. Производная функции $f (x)$ в точке $x_{0}$ - это предел отношений приращения функции к приращению аргумента, когда $∆ x \to 0$ . Данное определение записывается как $f' (x_{0}) = \lim_{∆ x \to 0} \frac{∆ f (x)}{∆ x}$ .

Если последний предел принимает конкретное значение, тогда существует конечная производная в точке. Когда предел бесконечен, то и сама производная бесконечна в этой точке. Когда предел не существует, то и производной в заданной точке не существует.

Функция $f (x)$ дифференцируема в точке $x_{0}$ , если конечная производная в ней существует.

Когда функция вида $f (x)$ дифференцируема в каждой точке из промежутка $(a; b)$ , тогда функцию называют дифференцируемой на заданном промежутке. Отсюда получаем, что любая точка $х$ из промежутка $(a; b)$ может принимать значения функции $f' (x)$ , иначе говоря, имеет место определение новой функции вида $f' (x)$ , которая называется производной функции $f (x)$ из интервала $(a; b)$ .

Нахождение производной иначе называют дифференцированием

Из выше указанного получаем, что производная в точке является числом, а производная функции на промежутке является функцией. Когда необходимо вычислять производную, обязательно обращаемся к нахождению переделов.

Пример 2

Найти производную функции $\sin (2 x)$ в точке $x_{0} = \frac{π}{6}$ .

Решение

Для нахождения производной в точке необходимо начать с написания предела отношения приращения функции к приращению аргумента, применив тригонометрические формулы. Получаем, что

$(\sin (2 x_{0}))' = \lim_{∆ x \to 0} \frac{∆ \sin (2 x_{0})}{∆ x} = \lim_{∆ x \to 0} \frac{\sin (2 (x_{0} + ∆ x)) - \sin (2 x_{0})}{∆ x} = = \lim_{∆ x \to 0} \frac{2 \cdot \sin \frac{2 (x_{0} + ∆ x) - 2 x_{0}}{3} \cdot \cos \frac{2 (x_{0} + ∆ x) + 2 x_{0}}{2}}{∆ x} = = 2 \cdot \lim_{∆ x \to 0} \frac{\sin (∆ x) \cdot \cos (2 x_{0} + ∆ x)}{∆ x}$

Для упрощения используем первый замечательный предел и в результате получаем, что

$(\sin (2 x_{0}))' = 2 \cdot \lim_{∆ x \to 0} \frac{\sin (∆ x) \cdot \cos (2 x_{0} + ∆ x)}{∆ x} = = 2 \cdot \lim_{∆ x \to 0} \frac{\sin (∆ x)}{∆ x} \cdot \lim_{∆ x \to 0} \cos (2 x_{0} + ∆ x) = = 2 \cdot 1 \cdot \cos (2 x_{0} + 0) = 2 \cos (2 x_{0}) = 2 \cos (2 \cdot \frac{π}{6}) = = 2 \cos \frac{π}{3} = 2 \cdot \frac{1}{2} = 1$

Ответ: $(\sin (2 x_{0}))' = 1$ .

Пример 3

Найти производную функции $f (x) = \sqrt{3 x^{3} - 1}$ из промежутка $x \in (\frac{1}{\sqrt[3]{3}}; + \infty)$

Решение

Для поиска производной из интервала понимаем, что результат должен быть функцией. Тогда $x_{0} = x$ , где значение $х$ возьмем любое число из заданного промежутка $x \in (\frac{1}{\sqrt[3]{3}}; + \infty)$ . Из определения видно, что производной считают отношение приращения функции на приращение аргумента, который стремится к нулю. Запишем

$f' (x) = {(\sqrt{3 x^{3} - 1})}^{'} = \lim_{∆ x \to 0} \frac{f (x + ∆ x) - f (x)}{∆ x} = = \lim_{∆ x \to 0} \frac{\sqrt{3 (3 + ∆ x)^{3} - 1} - \sqrt{3 x^{3} - 1}}{∆ x} = <\frac{0}{0}>$

Получаем неопределенность в результате. Поэтому следует произвести домножение на сопряженное выражение для применения формул сокращенного умножения, приведения подобных слагаемых и последующим сокращением выражения. Тогда получим, что

$f' (x) = \lim_{∆ x \to 0} \frac{\sqrt{3 (x + ∆ x)^{3} - 1} - \sqrt{3 x^{3} - 1}}{∆ x} = = \lim_{∆ x \to 0} \frac{(\sqrt{3 (x + ∆ x)^{3} - 1} - \sqrt{3 x^{3} - 1}) (\sqrt{3 (x + ∆ x)^{3} - 1} + \sqrt{3 x^{3} - 1})}{∆ x \cdot (\sqrt{3 (x + ∆ x)^{3} - 1} + \sqrt{3 x^{3} - 1})} = = \lim_{∆ x \to 0} \frac{(\sqrt{3 (x + ∆ x)^{3} - 1}) - {(\sqrt{3 x^{3} - 1})}^{2}}{∆ x \cdot (\sqrt{3 (x + ∆ x)^{3} - 1} + \sqrt{3 x^{3} - 1})} = = \lim_{∆ x \to 0} \frac{3 (x + ∆ x)^{3} - 1 - (3 x^{3} - 1)}{∆ x \cdot (\sqrt{3 (x + ∆ x)^{3} - 1} + \sqrt{3 x^{3} - 1})} = = 3 \cdot \lim_{∆ x \to 0} \frac{3 x^{2} + 3 x ∆ x + (∆ x)^{2}}{\sqrt{3 (x + ∆ x)^{3} - 1} + \sqrt{3 x^{3} - 1}} = = 3 \cdot \frac{3 x^{2} + 3 x \cdot 0 + (0)^{2}}{\sqrt{3 (x + 0)^{3} - 1} + \sqrt{3 x^{3} - 1}} = \frac{9 x^{2}}{2 \sqrt{3 x^{3} - 1}}$

Ответ: ${(\sqrt{3 x^{3} - 1})}^{'} = \frac{9 x^{2}}{2 \sqrt{3 x^{3} - 1}}$ и $x \in (\frac{1}{\sqrt[3]{3}}; + \infty)$

Для решения таких примеров необходимо учитывать то, что область определения функции $f (x)$ может не совпадать с областью определения производной этой функции. Предыдущий пример имеет область определения вида $D (f (x)) : x \in [\frac{1}{\sqrt[3]{3}}; + \infty)$ , а производная определена на интервале $D (f (x)) : x \in (\frac{1}{\sqrt[3]{3}}; + \infty)$ . То есть при дифференцировании функция $f' (x)$ - это производная заданной функции $f (x)$ из промежутка $x \in \{\begin{cases} D (f (x)) \\ D (f' (x)) \end{cases}$ .

Получение формул таблиц производных основано на определении производной. Они достаточно удобны, что способствует скорейшему дифференцированию сложных выражений. Использование понятия производной применяют для доказательств правил дифференцирования.

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.