Взаимно обратные функции, обратимая функция, график обратной функции и примеры

Понятие обратной функции и ее определение в алгебре

Допустим, что у нас есть некая функция $y = f (x)$ , которая является строго монотонной (убывающей или возрастающей) и непрерывной на области определения $x \in (a; b)$ ; область ее значений $y \in (c; d)$ , а на интервале $(c; d)$ при этом у нас будет определена функция $x = g (y)$ с областью значений $(a; b)$ . Вторая функция также будет называться непрерывной и строго монотонной. По отношению к $y = f (x)$ она будет обратной функцией. То есть мы можем говорить об обратной функции $x = g (y)$ тогда, когда $y = f (x)$ на заданном интервале будет либо убывать, либо возрастать.

Две этих функции, $f$ и $g$ , будут взаимно обратными.

Обратная функция – это что такое? Дадим определение взаимно обратимой функции (что такое обратимая функция - определение).

Для чего вообще нам нужно понятие обратных функций?

Это нужно нам для решения уравнений $y = f (x)$ , которые записываются как раз с помощью этих выражений. Также понятие особенностей обратных функций помогают в решении операций по извлечению n-ой степени (она обратна возведению в степень).

На самом деле это не является чем-то сложным. Онлайн, как и в нашем материале, вы можете найти много примеров обратной функции, которые помогут в этом убедиться.

Важно знать, что любая функция y = y (x) – это определенное правило, которое определяет соответствие между двумя значениями: x и y. К примеру, функция y = x² ставит соответственно каждому действительному числу его в квадрат. Можно сделать определенную таблицу, в которой будут располагаться значения этой функции для целых аргументов.

x	-2	-1	0	1	2
y = x²	4	1	0	1	4

Как найти функцию обратную данной

Как найти обратную функцию?

Допустим, нам нужно найти решение уравнения $\cos (x) = \frac{1}{3}$ . Его решениями будут все точки: $x = \pm a r с c o s (\frac{1}{3}) + 2 π \cdot k, k \in Z$

Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.

Разберем несколько задач на нахождение функций, обратных заданным. Вот несколько примеров обратной функции.

Пример 1

Условие: какая функция будет обратной для $y = 3 x + 2$ ?

Решение

Область определений и область значений линейной функции, данной в условии, – это множество всех действительных чисел. Попробуем решить данное уравнение через $x$ , то есть выразив $x$ через $y$ .

Мы получим $x = \frac{1}{3} y - \frac{2}{3}$ . Это и есть нужная нам обратная функция, но y здесь будет аргументом, а $x$ - функцией. Переставим их, чтобы получить более привычную форму записи:

$y = \frac{1}{3} x - \frac{2}{3}$

Ответ: функция $y = \frac{1}{3} x - \frac{2}{3}$ будет обратной для $y = 3 x + 2$ .

Обе взаимообратные функции можно отобразить на графике следующим образом:

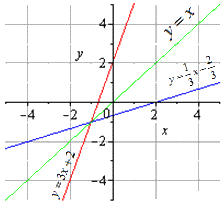
На графике мы находим симметричность обоих графиков относительно $y = x (о н и о т о б р а ж а ю т с я с и м м е т р и ч н о)$ . Эта прямая является биссектрисой первого и третьего квадрантов. Что это позволило нам доказать? Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.

Возьмем онлайн-пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.

Пример 2

Условие: определите, какая функция будет обратной для $y = 2^{x}$ .

Решение

Для заданной функции областью определения являются все действительные числа. Область значений лежит в интервале $(0; + \infty)$ . Теперь нам нужно выразить $x$ через $y$ , то есть решить указанное уравнение через $x$ . Мы получаем $x = \log_{2} y$ . Переставим переменные и получим $y = \log_{2} x$ .

В итоге этого примера у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.

Ответ: $y = \log_{2} x$ .

Графически обе функции будут выглядеть или иметь следующее отображение:

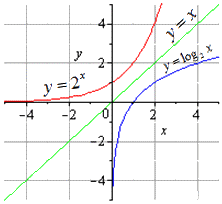
Также взаимно обратные функции можно рассматривать на примере теорем.

Предположим, мы имеем определенную, с возрастающей или убывающей монотонностью, а также непрерывную в определенном промежутке x функцию y = f(x). Значит, в промежутке значений y этой функции существует и обратная функция. Она также монотонно убывает или возрастает. Также ее можно определить как непрерывную (в промежутке y).

Основные свойства взаимно обратных функций

В этом пункте мы перечислим основные свойства обратимых функций $y = f (x)$ и $x = g (y)$ . Какими же свойствами обладают взаимообратные функции?

Определение 1

Первое (исходное) свойство мы уже вывели ранее: $y = f (g (y))$ и $x = g (f (x))$ .
Второе свойство вытекает из первоначального (первого) и означает, что область определения $y = f (x)$ будет совпадать с областью значений обратной функции $x = g (y)$ , и наоборот.
Графики обратных функций будут симметричными (находиться в симметрии) относительно $y = x$ .
Если $y = f (x)$ является возрастающей, то и $x = g (y)$ будет возрастать, а если $y = f (x)$ убывает, то убывает и $x = g (y)$ .

Советуем внимательно отнестись к понятиям области определения и области значения функций и никогда их не путать, так как это не одно и тоже даже исходя из названий. Допустим, что у нас есть две взаимно обратные функции $y = f (x) = a^{x}$ и $x = g (y) = \log_{a} y$ . Согласно первому свойству, $y = f (g (y)) = a^{\log_{a} y}$ . Данное равенство будет верным только в случае положительных значений $y$ , а для отрицательных логарифмов не определен, поэтому не спешите записывать, что $a^{\log_{a} y} = y$ . Обязательно проверьте и добавьте характеристику, что это верно только при положительном $y$ .

А вот равенство $x = f (g (x)) = \log_{a} a^{x} = x$ будет верным при любых действительных значениях $x$ .

Не забывайте про этот момент, особенно если приходится работать с тригонометрическими и обратными тригонометрическими функциями. Так, $a r c \sin (\sin (\frac{7 π}{3})) \neq \frac{7 π}{3}$ , потому что область значений арксинуса $[- \frac{π}{2}; \frac{π}{2}]$ и $\frac{7 π}{3}$ в нее не входит. Верной будет запись

$a r c \sin (\sin (\frac{7 π}{3})) = a r c \sin (\sin (2 π + \frac{π}{3})) = = {п о ф о р м у л е п р и в и д е н и я} = a r c \sin (\sin \frac{π}{3}) = \frac{π}{3}$

А вот $\sin (a r c \sin (\frac{1}{3})) = \frac{1}{3}$ – верное равенство, т.е. $\sin (a r c \sin x) = x$ при $x \in [- 1; 1]$ и $a r c \sin (\sin x) = x$ при $x \in [- \frac{π}{2}; \frac{π}{2}]$ . Всегда будьте внимательны с областью значений и областью определений обратных функций!

Графики взаимно обратных функций

Основные взаимно обратные функции: степенные

Если у нас есть степенная функция $y = x^{a}$ , то при $x > 0$ степенная функция $x = y^{\frac{1}{a}}$ также будет обратной ей. Замена букв будет давать соответственно $y = x^{a}$ и $x = y^{\frac{1}{a}}$ .

Сделаем график. На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):

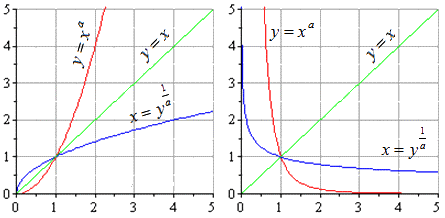
Основные взаимно обратные функции: показательные и логарифмические

Возьмем a, которое будет положительным числом, не равным $1$ .

Узнаем, какими будут графики для функций с $a > 1$ и $a < 1. О н и$ будут выглядеть так:

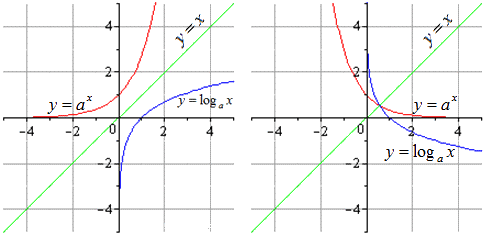
Основные взаимно обратные функции: тригонометрические и обратные тригонометрические

Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):

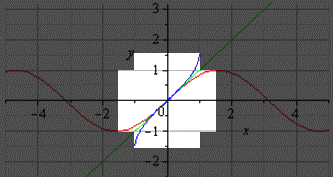
Если построить график главной ветви косинуса и арккосинуса, то он будет выглядеть так:

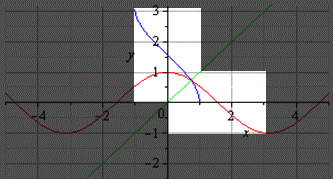
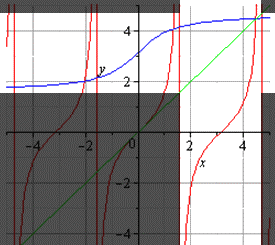
Если строить график главной ветви арктангенса и тангенса, то он будет таким:

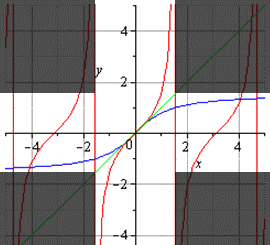
График главной ветви арккотангенса и котангенса будет таким:

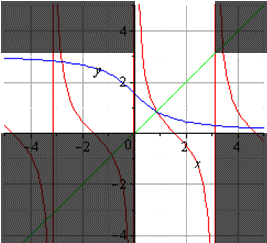
В случае построения обратных ветвей, отличные от главных, то обратную тригонометрическую функцию мы сдвигаем вдоль оси $O y$ на нужное число периодов. Так, если требуется обратная функция для ветви тангенса на $(\frac{π}{2}; \frac{3 π}{2})$ , то мы можем сдвинуть ее на величину $π$ вдоль оси абсцисс. График будет представлять собой ветвь арктангенса, которая сдвинута на $π$ вдоль оси ординат.