Нахождение длины вектора, примеры и решения

Содержание:

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Длина вектора - основные формулы

Длину вектора $\vec{a}$ будем обозначать $|\vec{a}|$ . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат $O x y$ . Пусть в ней задан некоторый вектор $\vec{a}$ с координатами $(a_{x}; a_{y})$ . Введем формулу для нахождения длины (модуля) вектора $\vec{a}$ через координаты $a_{x}$ и $a_{y}$ .

От начала координат отложим вектор $\vec{O A} = \vec{a}$ . Определим соответственные проекции точки $A$ на координатные оси как $A_{x}$ и $A_{y}$ . Теперь рассмотрим прямоугольник $O A_{x} A A_{y}$ с диагональю $O A$ .

Длина вектора - основные формулы

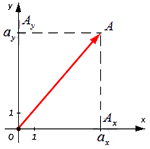
Из теоремы Пифагора следует равенство $O A^{2} = O {A_{x}}^{2} + O {A_{y}}^{2}$ , откуда $O A = \sqrt{O {A_{x}}^{2} + O {A_{y}}^{2}}$ . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что $O {A_{x}}^{2} = {a_{x}}^{2}$ и $O {A_{y}}^{2} = {a_{y}}^{2}$ , а по построению длина $O A$ равна длине вектора $\vec{O A}$ , значит, $\vec{|O A|} = \sqrt{O {A_{x}}^{2} + O {A_{y}}^{2}}$ .

Отсюда получается, что формула для нахождения длины вектора $\vec{a} = (a_{x}; a_{y})$ имеет соответствующий вид: $\vec{|a|} = \sqrt{{a_{x}}^{2} + {a_{y}}^{2}}$ .

Если вектор $\vec{a}$ дан в виде разложения по координатным векторам $\vec{a} = a_{x} \cdot \vec{i} + a_{y} \cdot \vec{j}$ , то вычислить его длину можно по той же формуле $\vec{|a|} = \sqrt{{a_{x}}^{2} + {a_{y}}^{2}}$ , в данном случае коэффициенты $a_{x}$ и $a_{y}$ выступают в роли координат вектора $\vec{a}$ в заданной системе координат.

Пример 1

Вычислить длину вектора $\vec{a} = (7; \sqrt{e})$ , заданного в прямоугольной системе координат.

Решение

Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам $\vec{|a|} = \sqrt{{a_{x}}^{2} + {a_{y}}^{2}}$ : $\vec{|a|} = \sqrt{7^{2} + {(\sqrt{e})}^{2}} = \sqrt{49 + e}$

Ответ: $\vec{|a|} = \sqrt{49 + e}$ .

Формула для нахождения длины вектора $\vec{a} = (a_{x}; a_{y}; a_{z})$ по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

Длина вектора - основные формулы

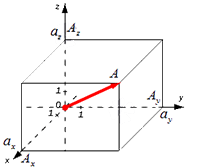
В данном случае $O A^{2} = O {A_{x}}^{2} + O {A_{y}}^{2} + O {A_{z}}^{2}$ (так как ОА – диагональ прямоугольного параллелепипеда), отсюда $O A = \sqrt{O {A_{x}}^{2} + O {A_{y}}^{2} + O {A_{z}}^{2}}$ . Из определения координат вектора можем записать следующие равенства $O A_{x} = a_{x}; O A_{y} = a_{y}; O A_{z} = a_{z};$ , а длина ОА равна длине вектора, которую мы ищем, следовательно, $\vec{|O A|} = \sqrt{O {A_{x}}^{2} + O {A_{y}}^{2} + O {A_{z}}^{2}}$ .

Отсюда следует, что длина вектора $\vec{a} = (a_{x}; a_{y}; a_{z})$ равна $\vec{|a|} = \sqrt{{a_{x}}^{2} + {a_{y}}^{2} + {a_{z}}^{2}}$ .

Пример 2

Вычислить длину вектора $\vec{a} = 4 \cdot \vec{i} - 3 \cdot \vec{j} + 5 \cdot \vec{k}$ , где $\vec{i}, \vec{j}, \vec{k}$ - орты прямоугольной системы координат.

Решение

Дано разложение вектора $\vec{a} = 4 \cdot \vec{i} - 3 \cdot \vec{j} + 5 \cdot \vec{k}$ , его координаты равны $\vec{a} = (4, - 3, 5)$ . Используя выше выведенную формулу получим $\vec{|a|} = \sqrt{{a_{x}}^{2} + {a_{y}}^{2} + {a_{z}}^{2}} = \sqrt{4^{2} + (- 3)^{2} + 5^{2}} = 5 \sqrt{2}$ .

Ответ: $\vec{|a|} = 5 \sqrt{2} .$

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами $A (a_{x}; a_{y})$ и $B (b_{x}; b_{y})$ , отсюда вектор $\vec{A B}$ имеет координаты $(b_{x} - a_{x}; b_{y} - a_{y})$ значит, его длина может быть определена по формуле: $\vec{|A B|} = \sqrt{(b_{x} - a_{x})^{2} + (b_{y} - a_{y})^{2}}$

А если даны точки с заданными координатами $A (a_{x}; a_{y}; a_{z})$ и $B (b_{x}; b_{y}; b_{z})$ в трехмерном пространстве, то длину вектора $\vec{A B}$ можно вычислить по формуле

$\vec{|A B|} = \sqrt{(b_{x} - a_{x})^{2} + (b_{y} - a_{y})^{2} + (b_{z} - a_{z})^{2}}$

Пример 3

Найти длину вектора $\vec{A B}$ , если в прямоугольной системе координат $A (1, \sqrt{3}), B (- 3, 1)$ .

Решение

Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим $\vec{|A B|} = \sqrt{(b_{x} - a_{x})^{2} + (b_{y} - a_{y})^{2}}$ : $\vec{|A B|} = \sqrt{(- 3 - 1)^{2} + (1 - \sqrt{3})^{2}} = \sqrt{20 - 2 \sqrt{3}} .$

Второй вариант решения подразумевает под собой применение данных формул по очереди: $\vec{A B} = (- 3 - 1; 1 - \sqrt{3}) = (- 4; 1 - \sqrt{3})$ ; $\vec{|A B|} = \sqrt{(- 4)^{2} + (1 - \sqrt{3})^{2}} = \sqrt{20 - 2 \sqrt{3}} .$ -

Ответ: $\vec{|A B|} = \sqrt{20 - 2 \sqrt{3}} .$

Пример 4

Определить, при каких значениях длина вектора $\vec{A B}$ равна $\sqrt{30}$ , если $A (0, 1, 2); B (5, 2, λ^{2})$ .

Решение

Для начала распишем длину вектора $\vec{A B}$ по формуле: $\vec{|A B|} = \sqrt{(b_{x} - a_{x})^{2} + (b_{y} - a_{y})^{2} + (b_{z} - a_{z})^{2}} = \sqrt{(5 - 0)^{2} + (2 - 1)^{2} + (λ^{2} - 2)^{2}} = \sqrt{26 + (λ^{2} - 2)^{2}}$

Затем полученное выражение приравняем к $\sqrt{30}$ , отсюда найдем искомые $λ$ :

$\sqrt{26 + (λ^{2} - 2)^{2}} = \sqrt{30} 26 + (λ^{2} - 2)^{2} = 30 (λ^{2} - 2)^{2} = 4 λ^{2} - 2 = 2 и л и λ^{2} - 2 = - 2 λ_{1} = - 2, λ_{2} = 2, λ_{3} = 0 .$

Ответ: $λ_{1} = - 2, λ_{2} = 2, λ_{3} = 0 .$

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов $\vec{A B}$ , $\vec{A C}$ и угол между ними (или косинус угла), а требуется найти длину вектора $\vec{B C}$ или $\vec{C B}$ . В таком случае, следует воспользоваться теоремой косинусов в треугольнике $△ A B C$ , вычислить длину стороны $B C$ , которая и равна искомой длине вектора.

Рассмотрим такой случай на следующем примере.

Пример 5

Длины векторов $\vec{A B}$ и $\vec{A C}$ равны 3 и 7 соответственно, а угол между ними равен $\frac{π}{3}$ . Вычислить длину вектора $\vec{B C}$ .

Решение

Длина вектора $\vec{B C}$ в данном случае равна длине стороны $B C$ треугольника $△ A B C$ . Длины сторон $A B$ и $A C$ треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: $B C^{2} = A B^{2} + A C^{2} - 2 \cdot A B \cdot A C \cdot \cos ∠ (\vec{A B,} \vec{A C}) = 3^{2} + 7^{2} - 2 \cdot 3 \cdot 7 \cdot \cos \frac{π}{3} = 37 \Rightarrow B C = \sqrt{37}$ Таким образом, $\vec{|B C|} = \sqrt{37}$ .

Ответ: $\vec{|B C|} = \sqrt{37}$ .

Итак, для нахождения длины вектора по координатам существуют следующие формулы $\vec{|a|} = \sqrt{{a_{x}}^{2} + {a_{y}}^{2}}$ или $\vec{|a|} = \sqrt{{a_{x}}^{2} + {a_{y}}^{2} + {a_{z}}^{2}}$ , по координатам точек начала и конца вектора $\vec{|A B|} = \sqrt{(b_{x} - a_{x})^{2} + (b_{y} - a_{y})^{2}}$ или $\vec{|A B|} = \sqrt{(b_{x} - a_{x})^{2} + (b_{y} - a_{y})^{2} + (b_{z} - a_{z})^{2}}$ , в некоторых случаях следует использовать теорему косинусов.

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.